What is a p-value(Updated and extended version)

In this video I'm going to look at the
question: what is a p-value? I'm going to do one simple example
of finding the p-value, but this video is mainly about the
concept of the p-value. The p-value is a measure of the strength
of the evidence against the null hypothesis that is provided by our sample data. The p-value is the probability of
getting the observed value of the test statistic, or a value with even greater evidence
against the null hypothesis, if the null hypothesis is in fact true. So first of all the p-value is a probability and it is a probability calculated conditional
on the null hypothesis being true.

The definition is a bit of a mouthful, so
let's look at an example. Suppose we wish to carry out a test of the
null hypothesis that mu, the population mean, is equal to
some hypothesized value. And suppose that we are sampling from a
normally distributed population, where sigma is known. If that's the case, the appropriate test
statistic is this Z test statistic.

If this null hypothesis is in fact true, then mu is equal to mu_0, and this statistic will have the standard normal distribution. And so over here I have the distribution
of that Z test statistic, if the null hypothesis is true, and that is the standard normal distribution. Suppose for the sake of illustration that we get a sample and we find that
the value of the test statistic is 2.05. 2.05 Is right about here on the curve.

In this case our alternative hypothesis is that the population mean is greater
than the hypothesized value, and so large values of this test statistic are going to give us evidence against
the null hypothesis. The farther out in the right tail that
this test statistic is, the greater the evidence against the
null hypothesis. And recall that the p-value is the probability of getting the observed
value of the test statistic, or something with even greater evidence
against the null hypothesis, if the null hypothesis is true. So in this case, that's going to be the
probability, under the null hypothesis, of getting the observed value of the test statistic or something even farther out in the
right tail.

Or in other words, the area to the right of the observed test statistic. That is going to be be the p-value here. And if we went to software or a standard
normal table here we'd see that this is approximately 0.020. In this particular setting, the farther
out in the right tail the observed value of the test statistic is, the smaller the p-value, and the greater the evidence
against the null hypothesis.

And this is true in the more general setting. The smaller the p-value, the greater the
evidence against the null hypothesis. If we have a given significance level alpha, then we reject the null hypothesis if the p-value is less than or equal to
the significance level alpha. Or we could say that the evidence against
the null hypothesis is significant at the alpha level of significance.

And so we could consider alpha to be a cut-off level for significance. In the real world, we're
not always going to have an alpha level given to us, and then the situation is not quite so simple. If we do have a given significance level, then
situation is not as cut and dried. But it might help us come up with
a reasonable conclusion if we understand the distribution of the p-value.

For continuous test statistics, under the assumptions of the model, if the null hypothesis is true the p-value will have a uniform distribution between
0 and 1. And a little loosely speaking, any value between 0 and 1 is equally likely to occur, if the null hypothesis is true. And so if the null hypothesis is true, on average we're going to get a p-value of 0.5. But it also might help with our
interpretation if we know something about the distribution of the p-value when the null hypothesis is false.

So let's simulate a million samples to investigate the distribution of the
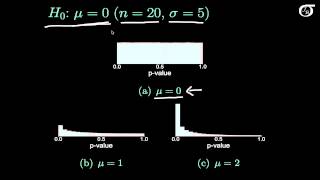
p-value in different scenarios. Here I've decided to test the null hypothesis that mu=0, against a two-sided alternative. The samples have 20 observations in them, and sigma is equal to 5. And we are sampling from a normally distributed population, so we'll be using as Z test.

And on this slide, there's three scenarios illustrated. In this first one, mu=0, so the true value of the population mean
is equal to the hypothesized mean, or in other words, the null hypothesis is true. Here's a histogram of the million p-values, corresponding to those million different samples that I've simulated. And as we can see, that p-value seems to
have that uniform distribution.

The theoretical average value for our
p-value when the null hypothesis is true is 0.5, And here in the simulation,
we also get a value of 0.50 To 2 decimal places. Down here I'm going to look at two
situations where the null hypothesis is false. In this first one, the true value of mu is 1, and we're still hypothesizing
that it's zero, so the null hypothesis is false. I've simulated a million samples where
mu is actually 1, and find out what the p-value is, and
plot it in this histogram.

And here the distribution is not uniform anymore, the distribution is moved towards 0. And in this situation, for those million p-values, we find an average p-value of 0.39. In this other situation, the null hypothesis is still false, but mu is even farther from the hypothesized value. And this histogram of p-values is
shifted even farther over toward 0, and the average p-value we got here is 0.18.

And so we can see here that when the
null hypothesis is true, the p-value has a uniform distribution
between 0 and 1, and when the null hypothesis is false,
the distribution of the p-value moves more toward zero. So we're going to be more likely to get p-values near 0 when the null hypothesis is false than when the null hypothesis is true. We saw here that the distribution of the
p-value depends on what the true value of the population mean is. It's also going to depend on the sample size, and the standard deviation in this case.

To illustrate that, let's see what happens when we increase
the sample size to 50. The only thing that's been changed in
this simulation is that the sample size has been
increased to 50. We can see here when the null hypothesis
is true that that distribution of the p-value is
still uniform between 0 and 1, and when the null hypothesis is false, the distribution of the p-value still, again, moves toward zero. But because of the increased sample size, down here when the null hypothesis is false, the p-value distribution has shifted
even farther towards 0.

Over here the average p-value is now 0.27, And over here the average p-value is now 0.04. When we have a greater sample size, our tests are going to have greater power, and the distribution of the p-value
is going to be shifted more toward 0. The overall lesson I'm trying to get at here is that we're more likely to get p-values
close to 0 when the null hypothesis is wrong than
when the null hypothesis is right. And so the smaller the p-value, the
greater the evidence against the null hypothesis.

I'm going to give a very rough guideline here. It has to be a very rough guideline because what we feel is strong evidence
against the null hypothesis depends on the situation at hand as well
as the p-value. But as a very rough guideline,
if the p-value is less than 0.01 We can say there is very strong evidence
against the null hypothesis. If the p-value lies between point 0.01 And 0.05, Well, there's starting to be strong
evidence against the null hypothesis.

If the p-value is between 0.05 And 0.10, There's some weak evidence against the
null hypothesis. And if the p-value is greater than 0.10 We
say there's little or no evidence against the null
hypothesis. This does depend on the setting.
If the p-value is close to 0.10, Some situations we may feel that that
has a hint of evidence against the null hypothesis.

For example, if our p-value is 0.11 Or 0.13 Or something like that, in some situations we might view that as a
hint of evidence against the null hypothesis. But for most practical cases once the
p-value starts getting up into the 0.2 And 0.3 Range and greater, we say that there is no evidence against
the null hypothesis..

Labels: UPDATE

Thanks for reading What is a p-value(Updated and extended version). Please share...!